Virtual Private Network (VPN)

Virtual Private Network ou em português Rede Particular Virtual, é uma rede de comunicação privada geralmente utilizada por uma empresa e/ou instituições, construída sobre a infra-estrutura de uma rede pública (normalmente a Internet). Ao invés de se utilizar links dedicados ou redes de pacotes (como Frame Relay e X.25) para conectar redes remotas, utiliza-se a infra-estrutura da Internet, não necessariamente segura.
Motivada pelo lado financeiro, onde os links dedicados são caros, e do outro lado está a Internet, que por ser uma rede de alcance mundial, tem pontos de presença espalhados pelo mundo.Conexões com a Internet podem ter um custo mais baixo que links dedicados, principalmente quando as distâncias são grandes, esse tem sido o motivo pelo qual, as empresas cada vez mais utilizam a infra-estrutura da Internet para conectar a rede privada.
A utilização da internet como infra-estrutura de conexão entre "hosts" da rede privada é uma ótima solução em termos financeiros, mas não em termos de privacidade, pois a internet é uma rede pública, onde os dados em trânsito podem ser lidos por qualquer equipamento.Como fica a segurança e a confidencialidade das informações da empresa? É tudo criptografado, assim incorporando a criptografia na comunicação entre hosts da rede privada de forma que, se os dados forem capturados durante a transmissãom, não possam ser decifrados. Os túneis virtuais habilitam o tráfego de dados criptografados pela internet e esses dispositivos entendem os dados criptografados, formando uma rede virtual segura sobre a internet.Os dispositivos responsáveis pelo gerenciamento da VPN devem ser capazes de garantir a privacidade, integridade, autenticidade dos dados.
Como funciona
 
O VPN pode ser efetuado de duas formas :
 
1ª  - Um simples host em trânsito, conecta em um provedor Internet e através dessa conexão, estabelece um túnel com a rede remota. A figura abaixo demonstra essa forma.

2ª - Duas redes se interligam através de hosts com link dedicado ou discado via internet, formando assim um túnel entre as duas redes. A figura 2 ilustra essa forma.

Figura 2: Conexão VPN entre duas redes interligadas.

Os protocolos utilizados no túnel virtual, são, (IPSec) Internet Protocol Security, (L2TP) Layer 2 Tunneling Protocol, (L2F) Layer 2 Forwarding e o (PPTP) Point-to-Point Tunneling Protocol. O protocolo escolhido, será o responsável pela conexão e a criptografia entre os hosts da rede privada. Eles podem ser normalmente habilitados através de um servidor Firewall ou RAS que esteja trabalhando com um deles agregado.
A figura 3 ilustra o caminho que os dados percorrem na arquitetura de rede do Windows sobre uma conexão VPN usando um modem analógico.

Figura 3: Passos numa conexão usando PPTP.

Um datagram IP, IPX, ou NetBEUI é submetido por seu protocolo apropriado à interface virtual que representa a conexão VPN, esta, usa o NDIS, que por sua vez, submete o pacote ao NDISWAN que codifica ou comprime e submete então ao protocolo PPTP, e este, ao formar o pacote resultado, envia pela interface serial que é usada pelo modem analógico.


Fontes: Wikipédia , Portal Chapeco e Universidad de Jaén
Espero que você tenha gostado, t+...

Ler artigo

DropBox

Dropbox é uma espécie de HD virtual com armazenamento online gratuito de até 2GB, com até 100GB disponível para clientes pagantes. Sincroniza automaticamente quando novos arquivos ou alterações são detectadas, sendo qualquer tipo e tamanho de arquivo, de qualquer software como Mac, Linux ou Windows.

Compartilhamento de arquivos é simples e pode ser feito com apenas alguns cliques.

• As pastas compartilhadas permitem que várias pessoas a colaborar em um conjunto de arquivos.
• Você pode ver as mudanças de outras pessoas instantaneamente. 
• A "pasta" Público que permite ligar diretamente para arquivos em seu Dropbox.
• Controle que é capaz de acessar pastas compartilhadas (incluindo a capacidade de chutar as pessoas para fora e remover os arquivos compartilhados a partir de seus computadores).
• Automaticamente crie galerias de fotos online partilhável das pastas de fotos em seu Dropbox.

Dropbox faz backup de seus arquivos online sem ter de pensar nisso. Uma cópia de seus arquivos são armazenados em servidores seguros do Dropbox. Isso permite que você acessá-los de qualquer computador ou dispositivo móvel.Ele tem a segurança e a privacidade de seus arquivos com muita seriedade. Além da aplicação Dropbox gratuitamente para o iPhone , IPad e Android.

Para usar ou obter mais informações visite o site DropBox.com .

Espero que tenha gostado do Post, t+ ...

Ler artigo

Cloud Computing (Computação nas Nuvens)

Cloud Computing

O nome Cloud Computing ou Computação nas Nuvens, se refere á ideia de utilizarmos em qualquer lugar, as variadas aplicações da internet com a mesma facilidade de tê-las instaladas em nossos próprios computadores.

Entenda a Computação Nas Nuvens

Estamos acostumados a utilizar aplicações instaladas em nossos micros e armazer arquivos e dados diversos nos micros.No ambiente geralmente corporativo, isto é um pouco diferente, já que nele é mais facil encontrar aplicações disponíveis em servidores e que podem ser acessadas por qualquer terminal com permissão atráves de uma rede.

Uma das principais vantagens deste modelo está no fato de ser possível, pelo menos na maioria das vezes, utilizar as aplicações mesmo sem estar conectado a internet ou a rede. Ou seja, é possivel usar estes recursos mesmo você estando off-line. Entretando todos os dados gerados estarão restritos a esse computador exceto quando compartilhamos em rede. Mesmo no ambiente corporativo, isso poder gerar algumas limitações, como a necessidade de se ter uma licença de um determinado software para cada computador, por exemplo.

Com a rápida e constante evolução da tecnologia computacional e das telecomunicações está fazendo com que o acesso à internet se torne cada vez maior e cada vez mais rápido. Em países mais desenvolvidos, como Japão, Alemanha e os EUA, é possivel ter acesso rápido à internet pagando-se muito pouco, assim criando uma situação perfeita para a popularização da Cloud Computing, embora esse conceito esteja se tornando conhecido no mundo todo, inclusive no Brasil.

Com a Cloud Computing, vários aplicativos, como arquivos e outros dados relacionados, não precisam mais estar intalados ou armazenados no seu computador.Elas passam a ficar disponíveis nas "nuvens", ou seja, na internet. Ao fornecedor da aplicação cabe todas as tarefas de desenvolvimento, armazenamento, manutenção, atualização, backup, escalonamento, etc.Você não precisará se preocupar com nada disso, apenas com acessar e utilizar.

Um bom exemplo prático da Cloud Computing é o Google Docs, serviço onde os usuários podem editar textos, fazer planilhas, elaborar apresentações de slides, armazenar arquivos, entre outros, tudo pela internet, sem necessidade de ter programas como o Microsoft Office ou OpenOffice.org instalados em suas máquinas. O que o usuário precisa fazer é apenas abrir o navegador de internet e acessar o endereço do Google Docs para começar a usar, não importa o sistema operacional ou o computador utilizado para esse fim. Neste caso, o unico cuidado que você deverá ter será o de usar um navegador de internet compativel, o que é o caso da maioria dos browsers da atualidade.

Tipoligia

Atualmente, a Cloud Computing é dividida em cinco tipos:

• IaaS - Infrastructure as a Service ou Infra-estrutura como Serviço (em português): quando se utiliza uma porcentagem de um servidor, geralmente com configuração que se adeque à sua necessidade.
• PaaS - Plataform as a Service ou Plataforma como Serviço (em português): utilizando-se apenas uma plataforma como um banco de dados, um web-service, etc. (p.ex.: Windows Azure).
•  DaaS - Development as a Service ou Desenvolvimento como Serviço (em português): as ferramentas de desenvolvimento tomam forma no cloud computing como ferramentas compartilhadas, ferramentas de desenvolvimento web-based e serviços baseados em mashup. 
• SaaS - Software as a Service ou Software como Serviço (em português): uso de um software em regime de utilização web (p.ex.: Google Docs , Microsoft Sharepoint Online). 
• CaaS - Communication as a Service ou Comunicação como Serviço (em português): uso de uma solução de Comunicação Unificada hospedada em Data Center do provedor ou fabricante (p.ex.: Siemens Enterprise , Locaweb).

 Fonte:Wikipédia e Info Wester
Espero que tenha gostado do post, t+...

Ler artigo

Impressora instantanea

O Instant cartucho de impressora é uma idéia incrível inspirado na linha de descartáveis como as câmeras são dispensados. O plano é comprar um cartucho de impressora da prateleira, de acordo com o tamanho de papel que planeja usar. Informações relacionadas a como a velocidade de impressão, resolução de impressão ea cor é fornecido na própria embalagem. Os designers e tentar trazer um eco-ângulo usando papel reciclável para a embalagem caixa de leite e peças recicláveis. No entanto, a impressora é alimentado por uma bateria interna e ganchos para o dispositivo e comp via USB.
Embora o conceito é bastante puro duvido que seria prático para pessoas como eu que passam por cartuchos de impressora mais rápida do que as recargas esferográfica!

Designers: Yuexun Chen & Chen Chia-Hsiao
Fonte:Yanko Design

Ler artigo

Imagem Fractal

Fractais (do latim fractus, fração, quebrado) são figuras da geometria
não-Euclidiana.

A geometria fractal é o ramo da matemática que estuda as propriedades e comportamento dos fractais. Descreve muitas situações que não podem ser explicadas facilmente pela geometria clássica, e foram aplicadas em ciência, tecnologia e arte gerada por computador. As raízes conceituais dos fractais remontam a tentativas de medir o tamanho de objetos para os quais as definições tradicionais baseadas na geometria euclidiana falham.

Um fractal (anteriormente conhecido como curva monstro) é um objeto geométrico que pode ser dividido em partes, cada uma das quais semelhante ao objeto original. Diz-se que os fractais têm infinitos detalhes, são geralmente autossimilares e independem de escala. Em muitos casos um fractal pode ser gerado por um padrão repetido, tipicamente um processo recorrente ou iterativo.

O termo foi criado em 1975 por Benoît Mandelbrot, matemático francês nascido na Polónia, que descobriu a geometria fractal na década de 1970 do século XX, a partir do adjetivo latino fractus, do verbo frangere, que significa quebrar.

Vários tipos de fractais foram originalmente estudados como objetos matemáticos.

História

Durante séculos, os objetos e os conceitos da filosofia e da geometria euclidiana foram considerados como os que melhor descreviam o mundo em que vivemos. A descoberta de geometrias não-euclidianas introduziu novos objetos que representam certos fenômenos do Universo, tal como se passou com os fractais. Assim, considera-se hoje que tais objetos retratam formas e fenômenos da Natureza.

A idéia dos fractais teve a sua origem no trabalho de alguns cientistas entre 1857 e 1913. Esse trabalho deu a conhecer alguns objetos, catalogados como "demônios", que se supunha não terem grande valor científico.

Em 1872, Karl Weierstrass encontrou o exemplo de uma função com a propriedade de ser contínua em todo seu domínio, mas em nenhuma parte diferenciável. O gráfico desta função é chamado atualmente de fractal. Em 1904, Helge von Koch, não satisfeito com a definição muito abstrata e analítica de Weierstrass, deu uma definição mais geométrica de uma função similar, atualmente conhecida como Koch snowflake (ou floco de neve de Koch), que é o resultado de infinitas adições de triângulos ao perímetro de um triângulo inicial. Cada vez que novos triângulos são adicionados, o perímetro cresce, e fatalmente se aproxima do infinito. Dessa maneira, o fractal abrange uma área finita dentro de um perímetro infinito.

Também houve muitos outros trabalhos relacionados a estas figuras, mas esta ciência só conseguiu se desenvolver plenamente a partir da década de 1960, com o auxílio da computação. Um dos pioneiros a usar esta técnica foi Benoît Mandelbrot, um matemático que já vinha estudando tais figuras. Mandelbrot foi responsável por criar o termo fractal, e responsável pela descoberta de um dos fractais mais conhecidos, o conjunto de Mandelbrot.

Categorias de Fractais

Os fractais podem ser agrupados em três categorias principais. Estas categorias são determinadas pelo modo como o fractal é formado ou gerado:

• Sistema de funções iteradas — Estas possuem uma regra fixa de substituição geométrica.
  


• Conjunto de Cantor, tapete de Sierpinski, Sierpinski gasket, curva de Peano, floco de neve de Koch, curva do dragão de Harter-Heighway, T-Square, esponja de Menger, são alguns exemplos deste tipo de fractal.
  


• Fractais definidos por uma relação de recorrência em cada ponto do espaço (tal como o plano complexo).
  


• Exemplos deste tipo são o conjunto de Mandelbrot e o fractal de Lyapunov.
  


• Estes também são chamados de fractais de fuga do tempo.
  


• Fractais aleatórios, gerados por processos estocásticos ao invés de determinísticos, por exemplo, terrenos fractais e o vôo de Lévy.
  

Ainda, também podem ser classificados de acordo com sua autossimilaridade. Existem três tipos de autossimilaridade encontrados em fractais:

• Autossimilaridade exata: é a forma em que a autossimilaridade é mais marcante, evidente. O fractal é idêntico em diferentes escalas. Fractais gerados por sistemas de funções iterativas geralmente apresentam uma autossimilaridade exata.



• Quase-autossimilaridade: é uma forma mais solta de autossimilaridade. O fractal aparenta ser aproximadamente (mas não exatamente) idêntico em escalas diferentes. Fractais quase-autossimilares contém pequenas cópias do fractal inteiro de maneira distorcida ou degenerada. Fractais definidos por relações de recorrência são geralmente quase-autossimilares, mas não exatamente autossimilares.
  


• Autossimilaridade estatística: é a forma menos evidente de autossimilaridade. O fractal possui medidas númericas ou estatísticas que são preservadas em diferentes escalas. As definições de fractais geralmente implicam alguma forma de autossimilaridade estatística (mesmo a dimensão fractal é uma medida numérica preservada em diferentes escalas). Fractais aleatórios são exemplos de fractais que possuem autossimilaridade estatística, mas não são exatamente nem quase autossimilares.
  

Entretanto, nem todos os objetos autossimilares são considerados fractais. Uma linha real (uma linha reta Euclidiana), por exemplo, é exatamente autossimilar, mas o argumento de que objetos Euclidianos são fractais é defendido por poucos. Mandelbrot argumentava que a definição de fractal deveria incluir não apenas fractais "verdadeiros" mas também objetos Euclidianos tradicionais, pois números irracionais em uma linha real representam propriedades complexas e não repetitivas.

Pelo fato do fractal possuir uma granulometria infinita, nenhum objeto natural pode sê-lo. Os objetos naturais podem exibir uma estrutura semelhante ao fractal, porém com uma estrutura de tamanho limitado.

Definições

Os fractais podem ser definidos segundo algumas características intuitivas, pois se torna difícil a conversão da definição matemática para a linguagem ordinária devido à falta de termos adequados à sua tradução.

Mandelbrot definiu fractal como "um sistema organizado para o qual a dimensão de Hausdorff-Besicovitch excede estritamente a dimensão topológica (número inteiro que caracteriza a geometria de um objeto euclidiano – por exemplo: zero para um ponto, um para uma linha, etc.), onde fractais cujas estruturas sejam ego-semelhantes, ou a dimensão de Hausdorff é igual a dimensão de Minkowski-Bouligand. Simplificando, o todo forma a parte e a parte forma o todo.

Na definição de fractal, os problemas de linguagem incluem:

* Não há nenhum significado preciso para o termo "muito irregular".
* Quando
se diz "dimensão", pode haver dúvida na definição do conceito, pois o termo pode
ter diversos significados (por exemplo: "tamanho", "importância, -no sentido de
valor-", "ordem de matrizes na representação matricial de um grupo", "grau",
"num espaço vetorial, o número de vetores de sua base", "num espaço, o número
mínimo de coordenadas necessárias à determinação unívoca de seus pontos", etc.).
Porém no caso dos fractais, dimensão significa estritamente o "número
fracionário ou irracional que caracteriza a geometria de um fractal.".
* Há
muitos modos que um objeto pode ser ego-semelhante. Pode-se tentar explicar como
uma espécie de fractais "irmãos gêmeos idênticos", onde existe a igualdade na
semelhança física, porém suas ‘personalidades’ são diferentes". Isto ocorre
quando inicialmente as curvas são alimentadas pelos mesmos dados, mas em
determinado momento, há um desvio nos valores dos dados, por exemplo, quando
observamos dois fractais numa escala 1:1, estes têm exatamente a mesma
aparência, mas se os observarmos numa dimensão 1:1.000.000, as figuras
observadas são completamente diferentes.
* Nem todo fractal possui
repetitividade, dependendo dos dados inseridos (principalmente no domínio do
tempo) este não terá em escalas menores a mesma aparência, aparecendo distorções
da figura.

Exemplos

Árvores e samambaias (ou fetos) são fractais naturais que podem ser modelados em computadores que usam algoritmos recursivos. Esta propriedade de recursividade ou repetitividade está clara nestes exemplos: num ramo de uma árvore ou na folhagem de uma samambaia pode ser observada uma réplica - não idêntica, porém semelhante na estrutura - em miniatura do todo .

Uma classe relativamente simples de exemplos é o Cantor que, observado num intervalo (digamos 1:1) e então noutro (1:10) mais curto (ou aberto), visto numa escala de 0, 1, é uma figura que pode ser (ou não ser) "ego-semelhante" em determinada amplificação, e pode (ou não) ter uma dimensão d ou 0 <>

Por exemplo, uma forma euclidiana normal - como um círculo - parece mais aplainada e alisada quando é amplificada. Numa ampliação infinita, seria impossível se diferenciar o círculo de uma linha reta. No caso dos fractais, isto não acontece (embora, também neste caso, quanto mais amplificarmos, mais nos aproximamos da linha reta) em razão da perda de dados ao longo de múltiplas amplificações (desvios acontecem pela imprecisão das inserções seqüenciais dos dados).

A idéia convencional de curvatura representada pela reciprocidade radial (em radianos) num círculo por aproximação, usualmente não pode ser aplicada em escalas muito grandes, pois o "raio" de curvatura fica fora de escala - daí a "aparência" de uma linha reta.

Com os fractais ocore o contrário: ao se aumentar a amplificação, revelam-se mais e mais os detalhes - a depender do grau de precisão e da quantidade de casas decimais dos dados inseridos. As distorções tendendo para a linha reta ocorrem justamente pelo fato de haver "falta de memória" nas máquinas que executam o cálculo. Portanto, um fractal jamais alcançará uma linha reta, salvo quando a fórmula que o constitui assim o permitir.

Alguns exemplos comuns de fractais:

Conjunto de Mandelbrot
Fractal de Lyapunov
Conjunto de Precentor
Tapete de Sierpinski
Triângulo de Sierpinski
Menger sponge
Curva de dragão
Curva de Peano
Curva de Koch

Os Fractais podem ser determinísticos ou estocásticos (Ver George G. Stokes).

No caso da Teoria do Caos, podemos associá-la totalmente aos fractais; também no conhecido "Mandelbrot set" Conjunto de Mandelbrot podemos observar discos inteiros, cuja dimensão é 2.

Isto não é de surpreender. O que é verdadeiramente surpreendente é que o limite do conjunto Mandelbrot também tem uma dimensão de Hausdorff de 2.

Aproximações de fractais (Fractais naturais) são encontradas freqüentemente na natureza. Estes objetos exibem uma estrutura complexa próxima aos objetos matemáticos, porém finitas, se as observarmos em escalas maiores.

Os fractais naturais estão à nossa volta, basta observarmos as nuvens, as montanhas, os rios e seus afluentes, os sistemas de vasos sanguíneos, os feixes nervosos, etc. Com maiores ou menores graus, estas figuras estão classificadas em diversas magnitudes.

Apesar de existirem por toda a natureza e de serem onipresentes, estes objetos somente foram realmente estudados a fundo no século XX.

Harrison [1] estendeu o cálculo Newtoniano para o domínio fractal, também inseriu os teoremas Gauss da divergência, o Teorema de Green, e o Teorema de Stoke.

Os Fractais são normalmente gerados através de computadores com softwares específicos. Através de seu estudo podemos descrever muitos objetos extremamente irregulares do mundo real. Como exemplo de softwares temos o Xaos -http://xaos.sourceforge.net/index.php.

Os meteorologistas utilizam o cálculo fractal para verificar as turbulências da atmosfera incluindo dados como nuvens, montanhas, a própria turbulência, os litorais, e árvores. As técnicas fractais também estão sendo empregadas para a compactação de imagens através da compressão fractal, além das mais diversas disciplinas científicas que utilizam o processo.

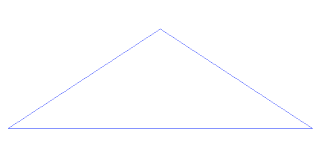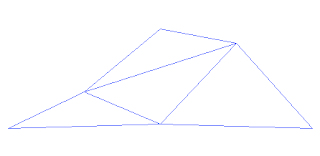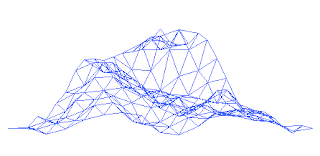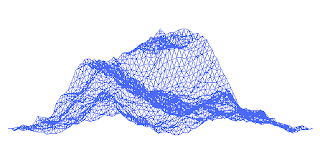
Montanhas Fractais

A superfície de uma montanha pode ser modelada num computador usando uma fractal: começamos com um triângulo no espaço 3D. Acham-se os pontos centrais das 3 linhas que formam o triângulo e criam-se 4 novos triângulos a partir desse triângulo. Deslocam-se depois aleatoriamente esses pontos centrais para cima ou para baixo dentro de uma gama de valores estabelecido. Vai-se repetindo o mesmo procedimento mas fazendo os deslocamentos dos pontos centrais dentro de uma gama de valores que em cada iteração é igual a metade da anterior.

Ler artigo

Pulseira Tecnológica

Saindo do mundo do cinema e voltando para a realidade, conheça agora o Mercator, uma pulseira despretensiosa à primeira vista, mas que é um projeto de um computador para múltiplas tarefas que usa nanotecnologia e holografia para agilizar a vida de seus usuários.

------------------------------------------------------------------------------------------------

Mercator

O dispositivo é um projeto da empresa de design de UI (interface de usuário) da cidade de ChengDu, na China. O equipamento combina alta tecnologia para servir de apoio a pessoas que são tão reféns da vida moderna que não podem perder tempo acessando um notebook para tarefas simples como ver email, saber a previsão do tempo, fazer lista de compras etc.

A intenção do equipamento não é substituir outros equipamentos como notebooks, netbooks, palms, tablets e desktops, contudo, ser um apoio para o dia a dia de qualquer cidadão atarefado. Ele torna mais simples e reúne várias funções corriqueiras em uma pulseira visualmente comum.
Ele se utiliza de projeção holográfica de imagens, nanotecnologia e nanomateriais como um novo processador em forma de chip da AMD™. Com isso, ele forma um bracelete simples que pode ser carregado no pulso tal qual uma pulseira convencional ou um relógio.
------------------------------------------------------------------------------------------------
Agenda

A vida moderna é corrida, isso é fato. Cada vez mais as pessoas têm menos tempo e acabam se perdendo em meio a tantos compromissos. O Mercator, se um dia se tornar realidade, coloca no pulso todas as tarefas que você precisa levar a cabo, evitando atrasos por ter se esquecido de uma ou outra atividade.

------------------------------------------------------------------------------------------------ Controle de saúde Além de informações como as citadas acima, o Mercator tem a capacidade de prestar informações sobre a saúde de seu utilizador, informando batimentos cardíacos, exibindo uma curva de sinais vitais e emitindo uma mensagem avisando se tudo vai bem ou não com o seu corpo.

------------------------------------------------------------------------------------------------
Mapas Ninguém mais fica parado e para quem se desloca diariamente por sua cidade ou então costuma viajar para lugares diferentes, o Mercator também conta com um sistema de mapas que indicam sua localização e permite a você acesso rápido a ruas e locais próximos de onde você se encontra.

Fonte:Kngyo Design

Espero que tenha gostado ... t+ !!

Ler artigo